J.ophthalmol.(Ukraine).2020;1:57-67.
|
http://doi.org/10.31288/oftalmolzh202015767 Received: 19 November 2019; Published on-line: 21 February 2020 Assessment of the efficacy of eyeball local vacuum compression with a new suction cup for impedance oculopneumoplethysmography depending on anatomical parameters of the eye A.G. Kovalchouk1, I.V. Potapenko2 1SI “The Filatov Institute of Eye Diseases and Tissue Therapy of the National Academy of Medical Sciences of Ukraine”; Odesa (Ukraine) 2 Odessa National I.I. Mechnikov University; Odesa (Ukraine) E-mail: alkov7@gmail.com TO CITE THIS ARTICLE: Kovalchouk AG, Potapenko IV. Assessment of the efficacy of eyeball local vacuum compression with a new suction cup for impedance oculopneumoplethysmography depending on anatomical parameters of the eye. J.ophthalmol.(Ukraine).2020;1:57-67. http://doi.org/10.31288/oftalmolzh202015767
The relationship between the eyeball size and convexity of its anterior part and the efficacy of local vacuum compression of the eye performed using a new design suction cup for impedance ophthalmopneumoplethysmography was studied. Based on the mathematical modeling of the geometric shape of the anterior segment of 75 eyes obtained by ultrasound biomicroscopy examination, it was found that the horizontal meridian curve of the anterior eye segment with a base diameter of 16.00 mm could be best approximated by a hyperbola. The surface area under the new suction cup with an inside diameter of about 16.5 mm was calculated using the formula for the segment surface area of a hyperboloid of revolution. It was determined by the convexity of the anterior part of the eye and varied from 247.3 to 271.4 mm2. The conversion coefficient of the level of applied vacuum to the level of IOP rise, calculated on the basis of individual combinations of the surface area of local vacuum compression and the eyeball size, was on average 0.83 ranging from 0.44 to 1.33. Using an individual conversion coefficient according to eyeball anatomical parameters will make it possible to measure diastolic ocular perfusion pressure during impedance OPPG with high sensitivity and accuracy. Keywords: impedance ophthalmopneumoplethysmography, mathematical modeling of the shape of the anterior eye, intraocular pressure, ocular perfusion pressure, local vacuum compression of the eyeball, ultrasound biomicroscopy
In the years of 2017-2018, Kovalchouk A.G. [1-3] provided substantiation of the potential for impedance oculopneumoplethysmography (OPPG) in diagnosing microvascular ciliary body ischemia by identifying low (< 35 mm Hg) diastolic ocular perfusion pressure (OPP) in the metarterioles of the ciliary body microvascular system. Diastolic OPP is identified by estimating, on the basis of the vacuum pressure applied, the increase in IOP at which a decrease in the pulsatile blood volume amplitude is registered by ocular rheography. The level of diastolic OPP in the metarterioles is close (slightly exceeds) to values of perfusion pressure at the arterial ends of capillaries, a decrease of which lower than 30-35 mm Hg leads to tissue ischemia. The proposed technique realizes an original approach to diagnosing the presence and degree of microcirculatory ischemia of the tissues through evaluating the level of a decrease in blood perfusion pressure at the arterial ends of capillaries. To perform a new technique, in 2016, Kovalchouk A.G. introduced an instrument for measuring perfusion pressure in the microvascular network of the ciliary body [4]. It has two noticeable weaknesses. Firstly, the device includes an L-shaped vacuum compression ring with the margins contacting with the sclera surface at acute angles and vacuum compression is accompanied by a lift of a sclera portion underneath. As a result, the wet conjunctiva, which covers the sclera, can contact the internal margins of the ring, thus, decreasing the area of local vacuum compression, reducing its efficacy, and destroying the linearity in converting the applied vacuum compression to the increase in IOP. Secondly, when using a vacuum compression ring with rheography electrodes installed on the pads opposite each other, it is impossible to achieve such level of applied vacuum which can induce a rise in IOP by 35 mm Hg, which is a necessary condition for measuring a maximum possible level of diastolic perfusion pressure in the metarterioles of the ciliary body in the norm. In 2017, a formula for the relationship between an increase in the IOP and level of local vacuum compression was obtained [2]. Below is an improved formula, the derivation of which is given in Appendix 1:
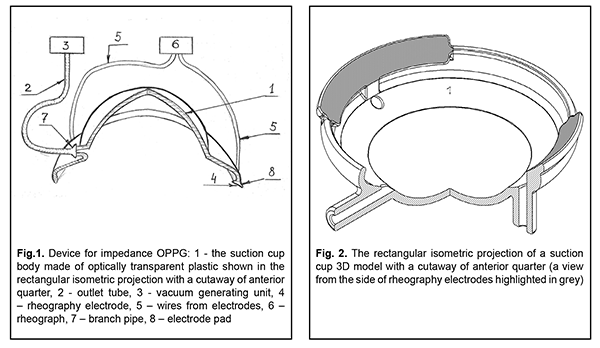
where P is the current IOP level during local vacuum compression of the globe (mm Hg), P0 is the baseline IOP level before local vacuum compression of the globe (mm Hg), ? is the coefficient that takes into account the efficacy of scleral deflection depending on the shape of the site of local vacuum compression, Svac is the area of local vacuum compression (mm?), VAC is the level of applied vacuum (mm Hg), R is the radius of the eye globe (a half of its axial length) (mm). During lamellar keratoplasty in order to increase IOP by 50 mm Hg, from 15 to 65 mm Hg, it is necessary to create vacuum no lower than 500 mm Hg. Respectively, to increase IOP by 35 mm Hg, from 15 to 50 mm Hg, vacuum required is 350 mm Hg, based on formula (1). In vacuum compression ring designed by Kovalchouk A.G. [4], two sectors, 80 degrees in size, are occupied by arcuated rheography electrodes installed on the pads opposite each other, which considerably decreases the area of vacuum compression. Consequently, a total area of vacuum compression, in comparison with a full vacuum compression ring, is decreased to (100 х 2) / 360 = 56%. According to formula (1), the increase in IOP is proportional to the squared area of local vacuum compression. Consequently, when the squared area of local vacuum compression is decreased down to 56%, which corresponds to a decrease of the factor Svac? in formula (1) to 31%, to increase IOP it is necessary to increase three-fold the level of vacuum compression under the vacuum-compression ring higher than 350 mm Hg, which is technically impossible since it exceeds the maximal possible vacuum value, 760 mm Hg. Previous papers [2, 3] have demonstrated that a suction cup with a round shape at the site of local vacuum compression is most effective for increasing IOP. It is against this background that Kovalchouk A.G has proposed a new device for impedance OPPG [5]. A block scheme of the device is given in Figure 1.
The device is composed of a suction cup with reography electrodes (1), a vacuum generating unit (3), and a rheograph (6). The suction cup is made of optically transparent plastic and designed as a cup in which: a central part is a segment of spherical shell with a radius and diameter of 7.7 mm and 12.0 mm, respectively, corresponding to the curvature and diameter of the cornea; a peripheral part between diameters of 12 and 19 mm is a spherical segment of spherical shell with a radius of 12.7 mm, an internal margin of which is connected with the central part and a free external margin is bent towards the axis of symmetry around a radius of 1.5-2.0 mm within a quadrant. In the central part of the suction cup at the site of connection with the peripheral part, there is a branch pipe (7) with an outlet tube (2) leading to the vacuum generating unit (3). Along the margin of and flash with the suction cup, there are two arcuated pads installed opposite each other. The contact surface of the pads is bent around a radius of 12.7 mm, which fits an average scleral curvature in the perilimbal area. On the pads, there are installed electrodes for reography (4). The electrodes are connected to the rheograph (6) by flexible wires (5). A free-from-electrode margin of the suction cup is rounded with a radius equal to half of its thickness. Variability in the shape of the anterior eye, caused by different eye prominence, can lead to significant changes in the area of local vacuum compression Svac under the newly designed suction cap; in addition, its size together with the size of the eyeball, according to formula (1), can have an effect on the level of local vacuum compression of the eyeball. The purpose of the present paper was to assess the efficacy of local vacuum compression of the eyeball performed with a new suction cup for impedance oculopneumoplethysmography depending on anatomical parameters of the eye. In the furtherance of this purpose, a 3D model of a new suction cup was designed based on Patent UA 131602. Figure 2 shows its rectangular isometric projection with a cutaway of the anterior quarter.
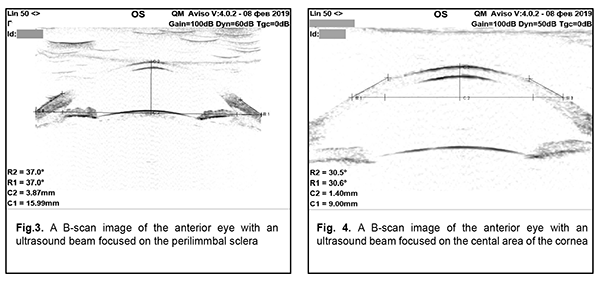
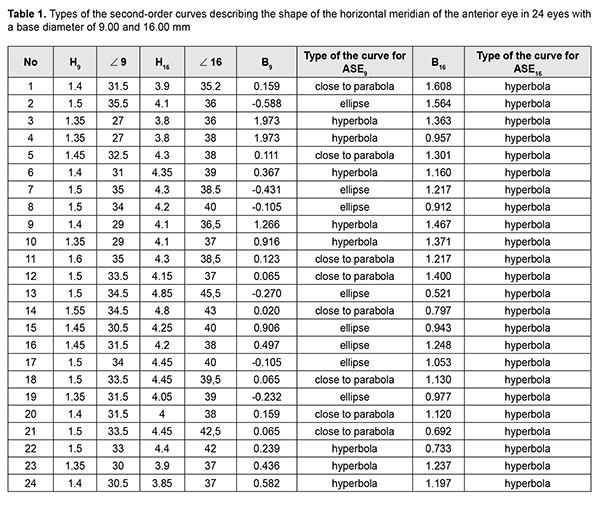
The suction cup has an external diameter of 19.0 mm and an average internal diameter of 16.5 mm. There is slight ovality caused by the fact that a diameter between the margins, with reography electrodes installed on them, is 16.0 and a diameter between the free margins is 17.0 mm. The internal diameter of the suction cup is smaller than the external one due to the thickness of a suction cup and a slope of a suction cup margin inward. The new suction cup is placed on the anterior part of the eye in such a way that the reography electrodes are positioned in upper and lower quadrants against the cornea. Herewith, the branch pipe with the outlet tube is always positioned from the temporal side and never bumps into projecting eye socket edges and the nose and the smaller internal diameter of the suction cup fits the vertical diameter of the cornea. The corneal diameters in horizontal and vertical meridians are approximately 11.7 mm and 10.6 mm, respectively [6]. Ovality (a) of the internal diameter of the new suction cup and a diameter of the cornea is calculated using the formula: where Dmax and Dmin – maximal and minimal diameter, respectively. According to formula (2), ovality of the internal diameter of the suction cup and the diameter of the cornea are approximately 6.1% and 9.9%, respectively. Close values in ovality of the internal suction cup diameter and the corneal diameter allow for congruence of the shape of the vacuum compression area and the cornea with the suction cup margins distanced from the corneal margins equally along the entire perimeter. In formula 1, Formula 3 shows that a coefficient of conversion of the level of the applied vacuum to the increase in IOP is influenced by two variables in addition to a constant coefficient ?: the area of vacuum compression and a radius of the eyeball equaling half of axial length. In this respect, for exact calculation of the increase in IOP, it is required to know precise values of the axial length and the area of the anterior part of the eye under the suction cup which consists of the cornea and the perilimbal sclera. Axial length can be easily measured using ultrasound or optic biometry. To measure the area of the anterior eye segment, it is necessary to know the geometrical shape of an eye. Thereby, a task was set to provide mathematical modeling of a shape of the anterior part of the eye by a second-order surface, which represents the closest approximation in shape. Material and Methods To achieve goal, forty patients (23 women and 17 men), aged from 15 to 76, with emmetropia and refractive errors (myopia, hypermetropia) were studied on a shape of the anterior eye (75 eyes) using two devices: an auto-ref-keratometer RC-5000 (Tomey) and an Aviso ultrasound unit (Quantel Medical). Inclusion criteria were as follows: 1) no previous history of ocular surgical procedures and eye injuries which could affect the shape of the anterior eye segment; 2) no changes in the corneal shape and size associated with congenital glaucoma, megalocornea, keratoconus; 3) corneal astigmatism within the physiological range (up to 0.75 D); 4) no changes in the shape of the perilimbal sclera associated with anterior staphyloma. An auto-ref-keratometer RC-5000 (Tomey) was used to measure i) the central radius of the corneal curvature in the strong and weak meridian (its mean value was used for further calculations) and ii) clinical refraction of the eye (spherical refractive equivalent was used for further calculations). An Aviso ultrasound unit (Quantel Medical) with a 50 MHz UBM probe with linear scanning was used to scan axially (coaxially to the optic axis) the anterior segment of the eye in a horizontal plane. In all patients, a B-scan image with an ultrasound beam focused at the perilimbal sclera showed the height H16 from the top of the cornea to the basement of the anterior eye segment with a diameter of 16.00 mm and angles of ?16 degrees between the contour line of a side surface of ASE and of its base diameter at the point of intersection (Figure 3). In addition, in thirteen patients (24 eyes), a B-scan image with an ultrasound beam focused at the central part of the cornea showed the height H9 from the top of the cornea to the basement of the anterior eye segment with a diameter of 9.00 mm and angles of ?9 degrees between the contour line of a side surface of ASE and of its base diameter at the point of intersection (Figure 4).
Nasal and temporal values of the angle could slightly differ from each other due to a slight decline of the ultrasound probe against the axial length. In this regard, the arithmetical mean of nasal and temporal values was used in calculations. The Aviso ultrasound unit was also used to perform ultrasound biometry and to measure axial length. A shape of the surface of the anterior eye segment was modeled using a second-order surface, where a curve given by the equation y = ?Ax + Bx2 was taken as a meridian. Results Depending on the value of the parameter B, the following variants of curves are possible: 1) B=-1 (circle), 2) B<0 (ellipse), 3) B=0±0.2 (parabola), 4) B>0 (hyperbola). The eccentricity of a meridian, being only dependent on the parameter B, completely defines the asphericity of a horizontal meridian in the anterior segment of the eye (ASE) with any base diameter. Table 1 demonstrates the measurements of heights (H) and angles (?) of the anterior eye segment with base diameters of 9 and 16 mm, the margins of which topographically correspond to the corneal periphery and external border of the perilimbal sclera, as well as these calculated parameters B9 and B16 for each of the twenty-four eyes.
Based on the literature data on the shape fit of the surface of the central cornea with the ellipsoid of revolution [7], the original hypothesis was a premise that the latter is also the best option to describe a geometric shape of the peripheral cornea, limbus, and perilimbal sclera. That premise was proved to be wrong. For ASE9, the best approximation of the curvature of the horizontal meridian was an ellipse, parabola, and hyperbola in 6, 8, and 10 cases, respectively. For ASE16, the best approximation of the horizontal meridian curvature was hyperbola in all cases. Consequently, the asphericity of the anterior eye surface in the horizontal meridian is growing (eccentricity is increased) with distance from the corneal top to the periphery. A diameter of 9.00 mm is, in fact, a transition zone of the horizontal meridian curvature from an ellipse in the center to a hyperbola in the periphery. The model obtained makes it possible not only to understand which model surface of revolution better fits the real surface of the eye but also to receive an approximate value of the area of eye surface with any diameter measured, which is important for various applications, in particular, for calculating a more precise level of an increase in IOP during local vacuum compression of the eyeball. The area of revolution surface (the axis of rotation, Ох) can be easily calculated using formula [8, page 217]:
In our case, we shall obtain for y = ? Ax + Bx2:
where H is a measured height of ASE. Thereafter, we shall describe a technique to find parameters A and B in the formula of revolution surface. Suppose (H) be the height of the anterior eye segment measured with a given diameter (d); ? be a measured angle between a tangent and a perpendicular, fallen from the point (H, d/2) on the axis (Ox); ? be an angle between a tangent and a positive direction of the axis (Ox), related to ? as ? = 90 °- ?. Thereupon, Hence, we shall obtain a system of linear algebraic equations for uknown parameters A and B:
Since a determinant of this system is
than in the system there exists an unambiguous solution, which can be found using Cramer formulas:
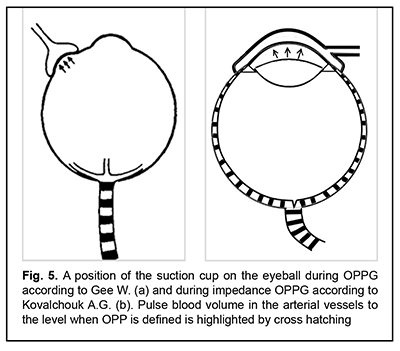
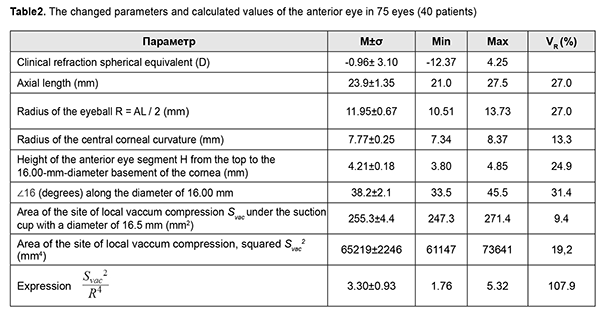
Measurements of the parameters in 75 eyes (40 patients) and the calculated values are given in Table 2. It should be noted that the size of the area of local vacuum compression (Svac) under the suction cup is completely defined by the height (H16) of the anterior eye segment and the angle (?16) between the contour line of a side surface and its base diameter at the point of their intersection, which together are characteristics of convexity of the anterior eye. Coefficients of correlation between Svac on the one side and H16 and ?16 on the other side were equal to 0.95 and 0.94, respectively (p<0.05). No correlation relationship was found between the axial length and H16 (r=-0.09) and between the axial length and ?16 (r=-0.06). A weak negative correlation relationship (r=-0.34) was found between Svac and a radius of the central corneal curvature (p<0.05). Relying on the data obtained, let us calculate for the new design suction cup a theoretical value of the conversion coefficient of the level of local vacuum compression to the increase of IOP as applied to an average-sized eye with AL of 23.9 mm and an average area of the anterior eye segment under the suction cup of 255.3 mm? and its possible extreme values (based on examination of 75 eyes). In the calculations, we will use the coefficient ?, which can be calculated according to the data on the dependence of the IOP increase level on the level of vacuum compression obtained by Ernest J.T. and colleagues when using a vacuum suction cup with an inside diameter of 13.0 mm applied to the inferotemporal scleral area of the globe. [9]. The possibility of using this coefficient ? for the new design vacuum suction cup is based on a premise that the ? value is determined only by the shape of the site of vacuum compression, which is round or alike in both vacuum suction cups. When performing ocular pneumoplethysmography in 40 eyes, Gee W. and colleagues [10] have found that the value of gradient slope of linear regression between the level of local vacuum compression within 100 to 300 mm Hg and the level of the increase in IOP varied from 0.148 to 0.318 (SD=0,041) with a mean value of 0.248, although the coefficient of correlation was very high (r>0.96) in all cases (p<0.02). In fact, gradient slope of linear regression between the level of local vacuum compression and the level of the increase in IOP is a conversion coefficient (K) which is individual for each eye. On the assumption that the mean value of gradient slope of 0.248 corresponds to the average size of the eye with axial length of 24.0 mm and, respectively, a radius of 12.0 mm, we shall calculate, using formula (2), a value of the constant coefficient (?) for a suction cup with an inside diameter of 13.0 mm. In the eye with AL of 24.0 mm, the size of the area of local vacuum compression (Svac) under the suction cup with an inside diameter of 13.0 mm and positioned on the sclera temporally from the cornea (Fig. 5, a) will be equal to the area of the surface of the spherical segment with a radius of 12.0 mm and a base radius r=13.0/2=6.5 mm:
A sought value of the coefficient ? for the suction cup with an inside diameter of 13.0 mm, according to formula (3), will be equal to:
Therefore, with a knowledge of the coefficient ? for a round shape of the site of local vacuum compression, the individual conversion coefficient (K) of the level of local vacuum compression to the level of the increase in IOP is readily calculated from formula (3) for each of 75 eyes with application of the new design suction cup (Fig. 5, b).
Table 1 demonstrates that the mean value of for the sample of 75 eyes was 3.3 with 5.32 and 1.76 as maximal and minimal values, respectively. If we apply the calculated value of the coefficient (?) to formula (3), we obtain the mean value of the conversion coefficient (K), equaling 0.83, with a variation range from 0.44 to 1.33 and oscillation of 107%. When an average conversion coefficient (0.83), without considering the variability of the anatomic parameters of the eyeball, is used for calculating a level of the increase in IOP, the maximal possible error can comprise from -47 % to +60 %. The absence of a correlation relationship (r=-0.09) between a radius of the eyeball (R) and the area of the site of vacuum compression (Svac) shows that it is necessary to take into the consideration the values of both independent variables when calculating the level of the increase in IOP. Lyubimov G.A. has calculated that when additional volume of liquid (?V) in amount from 10 to 100 mm3 is administered into the thin-walled spherical shell with a radius of 12 mm and with Young modulus of elasticity and thickness, typical for human eye, excess pressure inside increases in a linear fashion from 10 to 100 mm Hg [11]. Let us evaluate a size-average value of deflection of the sclera shell in the site of local vacuum compression (f?) with the maximally increased IOP by 35 mm Hg. This increase in IOP is required for measuring diastolic OPP in metarterioles which is observed in the norm. For this purpose, as calculated, it is required to administer inside the eye (to dislocate, in our case) the additional liquid in the amount of 35 mm3. Our previous papers [1, 2, 3] have demonstrated that the volume of dislocated liquid (?V) in local vacuum compression is equal to product of the area of local vacuum compression (Svac) and a height of scleral deflection of the sclera (averaged over the entire area of the local vacuum compression) (f?):
Consequently, an average height of deflection of the sclera shell in the entire area of local vacuum compression (f?) for the eye with a diameter of 24.0 mm with an average area of the anterior eye segment will be: (mm) The calculations show that deformation of the corneoscleral shell of the eye (f?) in the site of local vacuum compression is qualified as small since its value is twice smaller than the diameter of the eyeball with a ratio of
Elsheikh A. and colleagues have carried out corneal topography studies of the cornea with IOP elevated to approximately double the baseline levels using ophthalmodynamometer applanation and found that the maximum deflection height of the cornea was noted in the 2.5 mm wide corneal circumferential annulus next to the limbus while the shape in the center of the cornea with a diameter of 8.0 mm is almost unchanged [12]. The authors believe that the stability of the shape in the central area of the cornea with a diameter of 8.0 mm can be due to the higher stiffness, associated with a radial arrangement of collagen fibrils, while in the peripheral cornea the stiffness is reduced due to circular arrangement of collagen fibrils. We are of the opinion that flatness (a greater radius of curvature) of the cornea is of no less importance for a greater deflection height in the corneoscleral shell at the limbus and in the peripheral sclera as compared with the more convex central cornea. According to Laplace's law, other factors being equal, there is a greater local tension in the flattened area of the shell, which results in greater deformation and deflection height [13]. Due to the fact that the curvature is unchanged in the central cornea, deflection in the entire area of vacuum compression as to the baseline shape will be relatively uniform in height in the entire area. Local deflection of the corneoscleral shell, small in size and uniform in terms of area provides, in accordance with Hook's law, high linearity in conversion of the level of the applied vacuum to the level of the increase in IOP. By assuming that the value of coefficient ? is determined only by a shape of the site of local vacuum compression, formula (1) for dependence of the level of the increase in IOP on the level of the applied vacuum VAC for the round-shaped site of local vacuum compression will be expressed as follows: Following this formula, when the new design suction cup with an average inside diameter of 16.5 mm is used for increasing IOP by 35 mm Hg to the OPP level, specific to the norm, in an any size eye (providing that the sample of 75 eyes is representative) and with an estimated conversion coefficient of 0.44 to 1.33 (0.83, at average), it is required to create under the suction cup vacuum of 26 to 79.5 mm Hg (42. mm Hg, at average), which presents no technical difficulties. B-scan images of the anterior eye revealed that base diameter 16 mm in 61 eyes (81%) was positioned at the level of the iridociliary sulcus, which is an anterior edge of the ciliary body. In these patients, the new suction cup with an inside diameter of 16.0 mm in the sectors with rheography electrodes arranges these electrodes accurately above the ciliary body. In 14 eyes (19%), the base diameter 16 mm crossed the ciliary body pars plicata in the site from its first third to the posterior edge. This was caused by a smaller diameter of the cornea and the correspondingly decreased inside diameter of the ciliary body ring. In such cases, a suction cup with a smaller diameter must be used.
Discussion The proposed mathematical model for the shape of the anterior eye surface can be significantly improved if measurements and calculations of the eye asphericity are performed by several meridians along different meridians. Therefore, the calculated values of the area of the anterior eye surface will be more accurate. These accurate measurements can be performed using non-contact topography techniques for the anterior eye by Pentacam and OCT. If, as calculated using formula (4), the mean value of OPP during impedance OPPG in healthy eyes differs significantly from 35 mm Hg, it is required to correct a value of coefficient ? as appropriate. A need for correction will testify to the fact that a calculated value of the coefficient ? is in error due to inaccurate assessment of the average size of the eye in 40 patients as shown by Ernest J.T. and colleagues [8] or there are other factors, apart from the shape of local vacuum compression site, which influence the efficacy of conversion of the applied vacuum level to the IOP increase. The conviction that the association between the level of local vacuum compression and the level of the increase in IOP with the IOP level of 30 mm Hg is of a linear character is based on two experimental facts. First, Downs J.C. and colleagues have shown in experiment that the value of sclera deformation with the IOP level exceeding the physiological ranges (?30 mm Hg) becomes proportional to the level of the increase in IOP and explained it by the alignment of circumferential collagen fibrils of the sclera [14]. Second, Ernest J.T. and colleagues have performed local vacuum compression with simultaneous IOP measurements using Goldman’ tonometer in 40 eyes and found that, in each patient, a conversion coefficient of the vacuum compression level with the range of 100 to 300 mm Hg to the increase in IOP was characterized by a very high stability [8]. In all cases, the value of a conversion coefficient, individual for each patient, was unchanged in repeated measurements 15 minutes later. Taking into account the anatomical parameters of the eye will make it possible to significantly improve the accuracy in calculating the level of the increase in IOP depending on the level of local vacuum compression of the eyeball, which, in turn, will allow for highly sensitive and accurate measurements of diastolic OPP during impedance OPPG. Conclusions First, it was found, based on the mathematical medeling of the geometric shape of the corneal surface with circumferential perilimbal sclera using ultrasound biomicroscopy findings, that asphericity of the anterior eye surface in the horizontal meridian is growing (eccentricity is increased) with distance from the corneal center to the periphery and with the horizontal meridian curvature grading from an ellipse through a parabola to a hyperbola. For ASE16, the best approximation of the horizontal meridian curvature was a hyperbola in all cases. Second, the area of vacuum compression under the new design suction cup for impedance OPPG is completely defined by the height of the anterior segment of the eye with a base diameter of 16.5 mm and the angle between the contour line of a side surface and base diameter of the anterior segment of the eye at the point of their intersection, which together are characteristics of convexity of the anterior part of the eye. Third, the mean value of the site of local vacuum compression under the new suction cup, as calculated using the formula for the surface area of revolution hyperboloid, was 255.3±4.4 mm2 with a range of 24.3 to 271.4. Oscillation of the squared area of the site of vacuum compression under the new suction cup, entering into the formula for calculating the increase in IOP depending on the level of the applied vacuum, was 19.2%. A wide range of variants makes it necessary to take this parameter into account with the purpose to increase the accuracy in calculating the level of the IOP increase. Fourth, the absence of a correlation relationship (r=-0.09) between axial length and the area of vacuum compression shows that it is necessary to take into the consideration the values of both independent variables when calculating the level of the increase in IOP. Fifth, the value of coefficient ? for the scleral suction cup with an inside diameter of 13.0 mm, as calculated according to Ernest J.T. and colleagues, was equal to 0.248. This calculation is made on the assumption that the mean value of gradient slope of linear regression between the level of the applied vacuum and the level of the increase in IOP corresponds to the average size of the eyeball, 24.0 mm. By assuming that the value of coefficient ? is constant and only determined by the shape of the site of local vacuum compression, it can be used in the new suction cup for calculating the level of the increase in IOP Sixth, the conversion coefficient of the level of the applied vacuum to the level of IOP increase for the new design suction cup, calculated on the basis of individual combinations of the area of the local vacuum compression and axial length, averaged 0.83 ranging from 0.44 to 1.33. Consequently, for increasing IOP to the OPP level of 35 mm Hg, which is characteristic for physiologically normal condition, it is required to create under the suction cup the level of vacuum of 42 mm Hg ranging from 26 to 79.5 mm Hg. Seventh, a relatively small deflection of the corneoscleral shell of the eye in the site of vacuum compression (0.6% of AL), calculated for an eye with a diameter of 24.0 mm with the maximal increase in IOP to 35 mm Hg, according to Hooke's law, provides with a high linearity in conversion of the applied vacuum to the increase in IOP. Eighth, the suction cup of a new design has an inside diameter of 16.0 mm in the sectors with reography electrodes, which, in 81% of the cases (in the patients with a medium corneal diameter), enables the positioning of the electrodes accurately above the ciliary body. The eyes with larger or smaller corneal diameters will need suction cups of greater and smaller sizes, respectively. Finally, when an average conversion coefficient (0.83), without considering the variability of the anatomic parameters of the eyeball, is used for calculating a level of the increase in IOP, the maximal possible error can comprise from -47 % to +60 %. Using an individual conversion coefficient according to eye anatomical parameters makes it possible to measure diastolic ocular perfusion pressure during impedance OPPG with high sensitivity and accuracy. Abbreviations IOP – intraocular pressure OPP – ocular perfusion pressure AL – axial length ASEx – anterior segment of the eye with a basal diameter “x” ORG - ocular rheography OPPG – oculopneumoplethysmography UBM – ultrasound biomicroscopy
References: 1.Kovalchouk A.G. Theoretical justification of a new method in ciliary body microcirculatory ischemia diagnostics. National Journal glaucoma. 2017;16(4):69-78. (In Russ.) 2.Kovalchouk AG. Substantiating the potential for a new technique (impedance oculopneumoplethysmography) to diagnose microvascular ciliary body ischemia. J.ophthalmol.(Ukraine).2018;3:85-97. 3.Kovalchouk AG. [Substantiation of a New Method for Diagnosing Ciliary Body Microcirculatory Ischemia Based on Lower Diastolic Ocular Perfusion Pressure in Metarterioles] //Biofizika. 2018;63(4):812-24. In Russian. 4.Information Bulletin No. 23 issued 12.12.2016, based on Pat. of Ukraine №112192 issued 16.05.2016. [Instrument for non-invasive measuring of the perfusion pressure in the microvascular network of the ciliary body]. Author: Kovalchuk OG. Patent Holder: State Institution Filatov Institute of Eye Diseases and Tissue Therapy, NAMS of Ukraine. In Ukrainian. 5.Information Bulletin No. 2 issued 25.01.2019, based on Pat. of Ukraine №131602 issued 03.07.2018. [Instrument for non-invasive measuring of the perfusion pressure in the microvascular network of the ciliary body]. Author: Kovalchuk OG. Patent Holder: Kovalchuk OG. u201807455. In Ukrainian. 6.Vit VV. Vit VV. [The structure of the human visual system]. Odessa: Astroprint; 2003. 664p. In Russian. 7.Mandell RB, Helen StR. Mathematical model of the corneal contour. Br. J. Physiol. Opt. 1971;26:183-97. 8.Fihtengolts GM. [The course of differential and integral calculus]. Moscow: Nauka; 1966. 608p. In Russian. 9.Ernest J Terry, Desmond Archer, Alex E Krill. Ocular hypertension induced by scleral suction cup. Investigative Ophthalmology. 1972;11(1):29-34. 10.Gee William, Dale W Oller, Edwin J Wyllie. Noninvasive diagnosis of carotid occlusion by ocular pneumoplethysmography. Stroke. 1976;7:18-21. 11.Lyubimov GA. [On the role of rigidity in the development of intraocular pressure]. Glaucoma. 2006; 2:64–7. In Russian. 12.Elsheikh A, McMonnies CW, Whitford C, Boneham GC. In vivo study of corneal responses to increased intraocular pressure loading. Eye and Vision. 2015; 2(20). 13.Chung CW, Micha?el JA, Girard MJ, Jan NJ, Sigal IA. Use and Misuse of Laplace’s Law in Ophthalmology. Invest Ophthalmol Vis Sci. 2016;57(1):236-45. 14.Downs JC, Roberts MD, Burgoyne CF. Mechanical environment of the optic nerve head in glaucoma. Optom Vis Sci. 2008;85(6):425-35.
The authors did not receive funding when conducting research and writing an article. No Conflict of Interest is declared. Appendix No1 Derivation of refined formula for local vacuum compression of an eyeball In 2006, Lyubimov [11] presented a formula which showed the relationship between an increase in the pressure inside the sphere and an additional volume of fluid introduced into the sphere as applied to a mathematical model of the eye as a thin, spherical shell with biomechanical parameters of the human eye: where ?P is the increase in pressure (above atmospheric) inside the sphere expressed in mm Hg; E is the Young's modulus for the shell material expressed in megapascales (10-15 MPa); 0.73•104 is a coefficient of conversion of MPa to mm Hg t is the thickness of the spherical shell expressed in millimeters (0.5-1.0 mm); ?V is the increase in the volume of fluid inside the sphere expressed in cubic millimeters (10-100 mm3), R is the radius of the spherical shell expressed in millimeters. The mechanisms of the increase in IOP after injection of an additional volume of fluid into the eye and that after local vacuum compression of the sclera are different. In the former mechanism, the increase in IOP is associated with the increase in the volume of the intraocular fluid inside the sphera with a slight increase in the radius and maintenance of the spherical shape of the shell. In the latter mechanism, the increase in IOP is associated with slight local changes in the shape of the spherical shell with maintenance of the volume of the intraocular fluid. Under the condition that an increase in the IOP does not lead to changes in the shape of the eye outside the site of local compression by vacuum, displacement of a small volume of fluid under a vacuum-deformed scleral site can be considered as addition of a displaced volume of fluid to the total eye volume with a slight increase in eye radius in a uniform omnidirectional pattern and formula (1) can be used to determine the relationship between an increase in IOP and level of local vacuum compression. In a way similar to the injection of an additional volume of fluid into the spherical shell, the influence of vacuum on a local site of the sclera will be spread all over the sclera due to sliding of smooth margins of the ring-shaped suction cup on the conjunctiva with a free displacement of the underlying sclera (that, to a fist approximation, is a soft shell, if considered in the thickness direction) under the ring. It is obviously that the volume ?V of displaced fluid in this case will be equal to the area of the site of local vacuum compression Svac multiplied by the height of sclera deflection averaged over the entire area of the site f?,:
The height of scleral deflection averaged over the entire area of the site of local vacuum compression f? will be directly proportional to the area of the site of vacuum compression Svac and the level of applied vacuum VAC, taken with an additional coefficient ?; and inversely proportional to the Young's modulus E and scleral thickness t (with an increase in the values of the two latter parameters, vacuum causes less deformation in a stiffer scleral shell). The ? coefficient takes into consideration the efficacy of scleral deflection depending on the shape of the site of local vacuum compression.
where f? is the deflection of the scleral shell expressed in millimeters, ? is a coefficient that takes into consideration the efficacy of scleral deflection depending on the shape of the site of local vacuum compression Svac is the area of the site of vacuum compression expressed in mm?, VAC is the level of applied vacuum expressed in mm Hg, E is the Young's modulus for the shell material expressed in megapascales (10-15 MPa); 0.73•104 is is a coefficient of conversion of MPs to mm Hg t is the thickness of the spherical shell expressed in millimeters. Formula (3) is a special case of Hooke’s law, which is the basic law of elasticity, reflecting a linear relationship between the applied stress and small strains (or deformations) in an elastic medium. The deformation of the eye at the site of local vacuum compression is regarded as small since the maximum volume of displaced fluid (100 mm3) in a medium eye with a diameter of 24 mm is less than 1.4% of the eye volume. According to Hooke’s law, the formula for the deformation of elastic nail as a function of the applied force is a s follows:
where ?l is the absolute elongation or length decrease, F is the deformation force applied to the nail, k is the elastic coeffiient Let us compare formulas (3) and (4). The height of scleral deflection f? in the site of local vacuum compression in formula (3) corresponds to the value of linear deformation ?l,; the expression Svac•VAC in the numerator corresponds to F, the force of vacuum applied to the site of local vacuum compression, and the expression E•t in the denominator corresponds to the elastic (stiffness) coefficient for a thin, spherical shell filled with fluid. The additional coefficient ? in formula (3) takes into consideration the fact that the deformable elastic body represents the elastic thin-walled spherical shell, filled with water, the deflection height of which at the site of local vacuum compression is determined, all things being equal, by the shape of the site. The most effective shape is round because it provides the equal strain of the sclera shell along the edges which is the maximum possible for a given area. For example, the slope of the increase in IOP after the vacuum applied change for the suction cup with an inside diameter of 13 mm was found to be 0.248 [9]. A vacuum of at least 500 mm Hg is required for a 50 mm Hg rise in IOP (from 15 mm Hg to 65 mm Hg) for the ring-shaped suction cup (internal diameter, 12 mm; external diameter, 20 mm) used in laser in situ keratomileusis (LASIK). In this case, the slope of the IOP increase against the applied vacuum is about 0.1. Herewith, the area of vacuum compression under the hemispherical suction cup is 1.5 times less than that under the ring-shaped suction cup, 143.3 mm? versus 218.5 mm?, respectively. By replacing the height of scleral deflection f? in formula (2),
By replacing ?V in formula (1) with the equivalent expression from formula (5), and cancelling the variables that are present both in the numerator and denominator, we will obtain formula:
By replacing ?P in formula (6) with with the difference between current and baseline intraocular pressure, P-P0, we will obtain the formula for the relationship between the level of applied vacuum VAC and the level of the increase in IOP:
where P is the current IOP level during local vacuum compression of the globe (mm Hg), P0 is the baseline IOP level before local vacuum compression of the eyeball (mm Hg), ? is the coefficient that takes into consideration the effiacy of scleral deflection depending on the shape of the site of local vacuum compression, Svac is the area of the site of local vacuum compression (mm?), VAC is the level of applied vacuum (mm Hg), R is the radius (or a half of axial length) of the eye (mm)
|

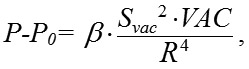 (1)
(1)
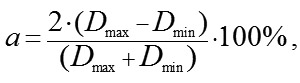 (2)
(2)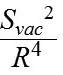 is, in fact, a coefficient
is, in fact, a coefficient 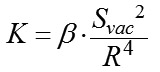 (3)
(3)
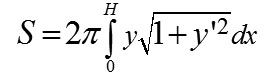
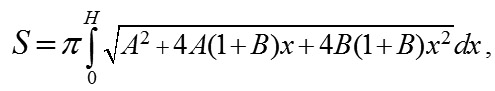
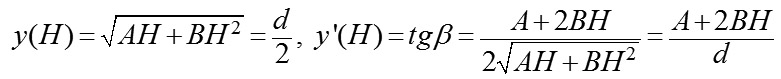
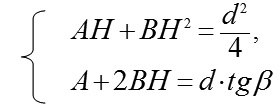
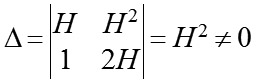
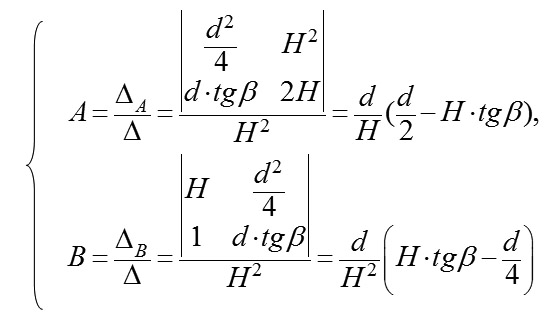
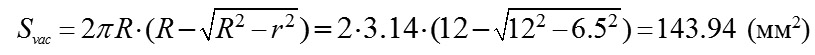
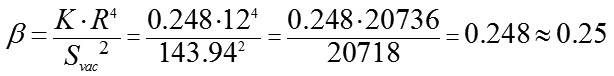
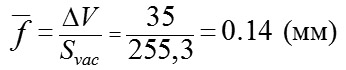
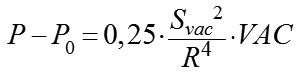 (4)
(4)
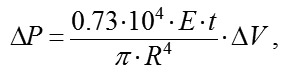
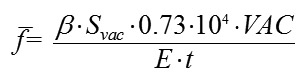
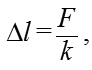
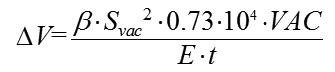 (5)
(5)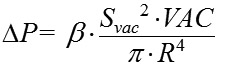 (6)
(6)